관성계와 회전계에서의 대기의 방정식

관성계에서의 대기의 지배방정식
(Governing Eqs in inertial framework)

대기를 표현할 수 있는 다양한 요소들: 기압(p), 온도(T), 밀도($\rho$), 3차원 바람들(u,v,w)로 서로 어떤 관계가 있는지를 표현하는 방정식을 대기의 지배방정식이라고 한다.

 

질량 보존(Mass Conservation Eq)

$$\frac{D\rho}{Dt} = -\rho \nabla \cdot \vec{V}$$

• $-\rho \nabla \cdot \vec{V}$은 대기의 수렴을 나타내는 항으로 양수이면 대기가 수렴하여 밀도가 높아지는 것을 나타내며 음수이면 대기가 발산하여 밀도가 낮아짐을 표현함

 

모멘텀 보존(Momentum Conservation Eq; Navier-Stokes Eq)

$$\frac{D\vec{V}}{Dt} = -\frac{1}{\rho} \nabla P + \vec{F} + \nu \nabla^2 \vec{V}$$

 

• $-\frac{1}{\rho} \nabla P$은 기압 경도력
• $\vec{F}$는 코리올리힘, 중력, 마찰력 등 외부에서 가한 힘(External Force)
• $\nu \nabla^2 \vec{V}$은 대기의 비압축성($\nabla \cdot \vec{V}$)을 가정하였을 때의 점성

 

열에너지 보존(Thermaldynamic Eq)

$$\frac{D\theta}{Dt} = \frac{1}{c_p} \frac{\theta}{T} \dot{Q}$$

 

• $\theta$는 온위(단열 과정을 따라 지상까지 공기가 이동했을 때의 온도)
• $C_p$는 정압비열
• $\dot{Q}$은 비단열 가열(Diabatic heating: 응결, 관입...)

단열과정(Adiabatic heating)에서는 $\dot{Q}=0$이기에 $\theta$는 변하지 않는다.

 

 

이상기체 방정식(Ideal gas Eq)

$$P=\rho R T$$

 

모멘텀 보존식 안에 u,v,w에 대한 3개의 식이 존재하기에 대기의 상태를 표현하는 총 6개의 방정식과 6개의 변수가 존재한다.

=> 위의 식과 변수들만으로도 해를 명시적으로 구할 수 있다.

 

점성이 없다고 가정하면 모멘텀 보존식에서 $\nu \nabla^2 \vec{V}$ 이 0이 되는데 이를 Euler equation으로 명명한다.

$$\frac{D\vec{V}}{Dt} = -\frac{1}{\rho} \nabla P + \vec{F}$$

점성은 다른 힘들에 비해 매우 작고 비선형적이라 연산이 어려기에 중규모 이상의 기상현상에서는 무시하여도 좋다. 난류와 같은 소규모에서는 제거하면 안 된다.

 

회전계에서의 대기의 지배방정식
(Governing Eqs in  Rotating framework)

그림 1. 회전계에서 정지한 물체가 받는 힘 실제 중력(g)와 겉보 중력($g_e$)

 

위의 그림과 같이 회전계에서 어떤 물체가 위치 r에 정지해있다고 가정하자. 관성계(고정계)에서 관측하였을 때 물체는 회전하는 것처럼 보이게 된다.
만일 무한소만큼 물체가 회전계에서 정지했다면 관성계에서는 다음 식만큼 움직일 것이다.
아랫첨자: I=관성계, R=회전계
$$(d\vec{r})_{I}= d\theta \times \vec{r} \tag{4}$$
양변을 $dt$로 나눠준다면 회전계에서 고정된 물체의 속도를 얻을 수 있다. 여기서 $\Omega$는 회전계의 회전각속도이다.
$$\left( \frac{D\vec{r}}{Dt} \right)_{\text{I}} = 
\left( \frac{D\vec{\theta}}{Dt} \right)_{\text{I}} \times \vec{r}
= \vec{\Omega} \times \vec{r} \tag{5}$$
만일 회전계 관점에서 물체가 속도 $(Dr/Dt)_R$만큼 가진다면 관성계와 회전계에서의 속도는 다음과 같은 관계를 갖는다.
$$\vec{V_I} = \left( \frac{D \vec{r}}{Dt} \right)_I = \left( \frac{D \vec{r}}{Dt} \right)_R + \vec{\Omega} \times \vec{r} = \vec{V_{R}} + \vec{\Omega} \times \vec{r} \tag{6}$$
$$\vec{V}_I = \vec{V}_R + \vec{\Omega} \times \vec{r} \quad\Rightarrow\quad \vec{V}_R = \vec{V}_I - \vec{\Omega} \times \vec{r} \tag{7}$$
두 속도의 전미분 또한 식. 6 가운데 등호와 같은 관계를 갖기에 다음과 같이 표현할 수 있다.
$$\left( \frac{D \vec{V}}{D t} \right)_I = \left( \frac{D \vec{V}}{D t} \right)_R + \vec{\Omega} \times \vec{V} \tag8$$
식 8.에 식 7.을 대입하면 다음과 같이 유도된다. 
이때 식 9.의 첫번째 줄에서 우변의 두번째 항은 매우 작기에 무시한다.
$$
\begin{align}
\left( \frac{D}{D t} \left( \vec{V_R} \right) \right)_I=\left( \frac{D}{D t} \left( \vec{V}_I - \vec{\Omega} \times \vec{r} \right) \right)_I
&= \left( \frac{D \vec{V}_I}{D t} \right)_I 
- {\frac{D \vec{\Omega}}{D t} \times \vec{r}} 
- \vec{\Omega} \times \left( \frac{D \vec{r}}{D t} \right)_I \\
&= \left( \frac{D \vec{V}_I}{D t} \right)_I 
- \vec{\Omega} \times \vec{V}_I \\
&= \left( \frac{D \vec{V}_I}{D t} \right)_I 
- \vec{\Omega} \times \vec{V}_R 
- \vec{\Omega} \times \left( \vec{\Omega} \times \vec{r} \right) \\
\end{align} 
\tag{9}
$$
또한 식 8.에 $\vec{V_R}$을 대입하면 다음과 같고
$$\left( \frac{D}{D t} \left( \vec{V_R} \right) \right)_I= \left(\frac{D}{Dt}\vec{V_R}\right)_{R}+ \vec{\Omega}\times \vec{V_{R}}\tag{10}$$
식 9.에 식 2-1(Euler equation)을 대입한 다음 식 10.과 엮으면 마침내 다음과 같은 관계식이 나온다!
$$
\left(\frac{D \vec{V}_R}{D t}\right)_R
= -\frac{1}{\rho} \nabla P + \vec{F}
- \underbrace{2 \vec{\Omega} \times \vec{V}_R}_{\text{Coriolis force}}
- \underbrace{\vec{\Omega} \times \left( \vec{\Omega} \times \vec{r} \right)}_{\text{Centrifugal force}} \tag{11}
$$
식 11.에서 첫번째와 두번째 항은 Euler equation과 동일하나 세번째와 네번째 항이 추가적으로 생성되었다.
세번째 항은 코리올리 힘(전향력)으로 물체가 움직여서 $\vec{V_{R}}>0$인 경우에만 작용하는 힘으로 그림 2.와 같이 북반구에서는 오른쪽, 남반구에서는 왼쪽으로 작용하게 된다.
네번째 항은 원심력으로 실제 중력(g)와 함께 작용하여 겉보기 중력($g_e$)을 형성한다.

그림 2. 코리올리 힘이 작용하는 방향

 

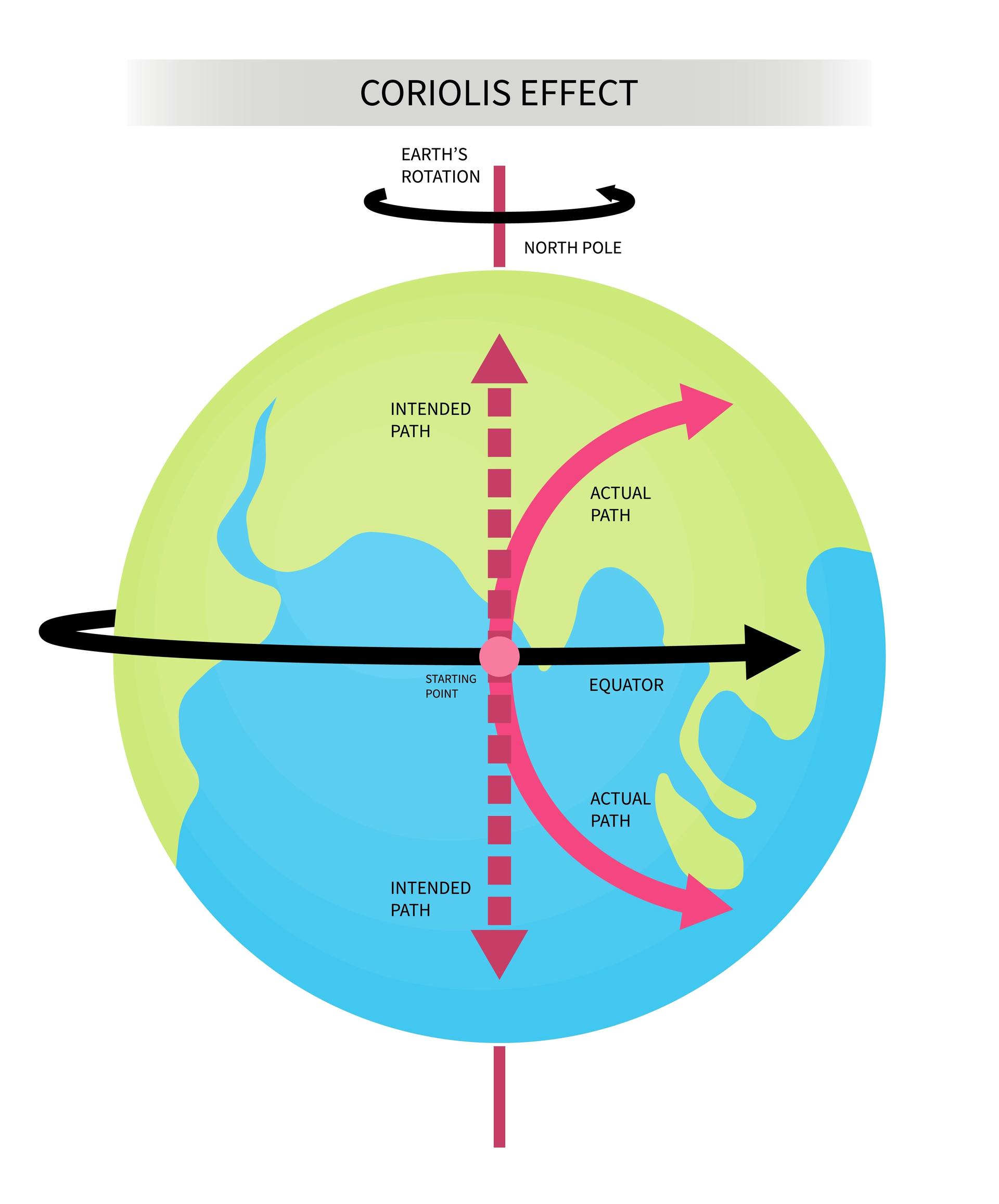
최종적으로 회전계에서의 대기 방정식을 정리하면 다음과 같다.

1. Mass Conservation
$$\frac{D \rho}{D t} = - \rho \nabla \cdot \vec{V}$$
2. Momentum Conservation
$$
\frac{D \vec{V}}{D t}
= -\frac{1}{\rho} \nabla P
- 2 \vec{\Omega} \times \vec{V}
+ \vec{g_{e}}\cdot\hat{k}
+ + \vec{F}_{except\_{g}}
- \vec{\Omega} \times \left( \vec{\Omega} \times \vec{r} \right)
$$
3. Thermodynamic
$$
\frac{D \theta}{D t}
= \frac{1}{c_p} \frac{\theta}{T} \dot{Q}
$$
4. Ideal gas
$$
P = \rho R T
$$

 

※출처

그림 1

https://www.meteo.physik.uni-muenchen.de/~roger/TCLecs/Tropical%20Cyclones_FD.html 

그림 2

https://www.piprocessinstrumentation.com/flowmeters/article/53076029/the-coriolis-flowmeter-principle-its-origin-and-meaning